Which equation represents the function graphed on the coordinate plane?Suppose we are given continuous on [a,b] function y=f(x) that is twice differentiable, except points where derivative f(x) doesnt exist or has infinite For better graph take a couple of control points: `(1,1),(1,1/2),(4,1/4)`. Since function is odd, reflect it about origin. Shift the function 1 unit to the right.The graph of a function f is the set of all points in the plane of the form (x, f(x)). We could Return to Contents. Characteristics of Graphs. Consider the function f(x) = 2 x + 1. We recognize the equation y = 2 x + 1 as the Slope-Intercept form of the equation of a line with slope 2 and y-intercept (0,1).8. Find The Critical Points For The Function F(x) - 12x-x. Transcribed Image Text from this Question. 7. Which graph represents the function f(x) = x(x - 1)(x-3)?It helps with understanding what the graph represents. We saw how to sketch such graphs in Graph of a Function. The function `f(x)` has a domain of "all real numbers, `x > 2`" as defined in the question. (There are no resulting square roots of negative numbers or divisions by zero involved here.)
Steps for Sketching the Graph of the Function on eMathHelp
Functions & Graphing Calculator. Analyze and graph line equations and functions step-by-step. f(x).A curve drawn in a graph represents a function, if every vertical line intersects the curve in at most one point. Question 1 : Determine whether the graph given below represent functions. Give reason for your answers concerning each graph. Solution : Since the graph intersects the vertical line (y-axis) at...answers to question: Which graph represents the function f(x) =three-halves(2)x? - on answers-learning.com. Which description is represented by a discrete graph? kiley bought a platter for $19 and several matching bowls that were $8 each. what is the total cost before tax? the temperature at 9...You've reached the end of your free preview. Want to read the whole page? TERM Spring '16. TAGS Derivative, Prime number, Inverse function, Logarithm, objective 2.5b.

Graphs of Functions
My question is how do we know that a given function's graph actually is what we think it is? I know for things like lines, circles and conics we can prove that Essentially the graph represents the function because it's defined that way. We choose to identify the function $f:X \rightarrow Y$ with the points...We have a ray that is reflected at the origin about the y-axis. Now, let's explore the different transformations for an absolute value graph by taking a y = |x + h What happens to the graph? Well, we have shifted the graph -h units, just like a normal trigonometric, linear, or even parabolic graph.In mathematics, the graph of a function f is the set of ordered pairs (x, y), where f(x) = y. In the common case where x and f(x) are real numbers, these pairs are Cartesian coordinates of points in two-dimensional space and thus form a subset of this plane.Purplemath. The last two easy transformations involve flipping functions upside down (flipping them around the x-axis), and mirroring them in the y-axis. To see how this works, take a look at the graph of h(x) = x2 + 2x - 3. The graph of the original function looks like this Graph A represents -f (x).The -3 is inside of the absolute value, which means that the parent function has been shifted to the left by 3 units. When we graph the given function, the answer is the graph shown below. Hope this helps!
This is a floor function graph(*3*)
For any x, flooring (x) is defined as the biggest integer not up to or equivalent to x(*3*)
For example, let x = 3 ....so....(*3*)
floor (3) = 3(*3*)
So(*3*)
flooring(3) - 3 = 0(*3*)
And let x = 2.5 .....so....(*3*)
flooring (2.5) = 2 (*3*)
So(*3*)
flooring (2.5) - 3 = 2 - 3 = -1(*3*)
The ultimate graph is correct(*3*)
(*3*)
Which graph represents the piecewise-defined function? {−4 ...

Which graph represents the function f(x) = 3-* +4? 10 8 -6 ...

Image 1: Which graph represents the function f(x)=√x-2−2 ...

Which graph represents the function f(x) = -|x+3 ...

Which graph represents the function f (2 x)? - Brainly.in

Which graph represents the function f(x) = (x-3 ...

Which graph represents the function f(x)=1/x+3-2 - Brainly.com

Which graph represents the function over the interval [−3 ...

Transformations of Functions Practice - MathBitsNotebook ...
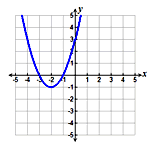
Which graph represents the polynomial function f(x)=x^3+3x ...

Which graph represents the function f(x) = -x + 3/?

Which graph represents the polynomial function f(x)=x^3+3x ...

Which graph represents the function f(x)=1/x+3-2 - Brainly.com
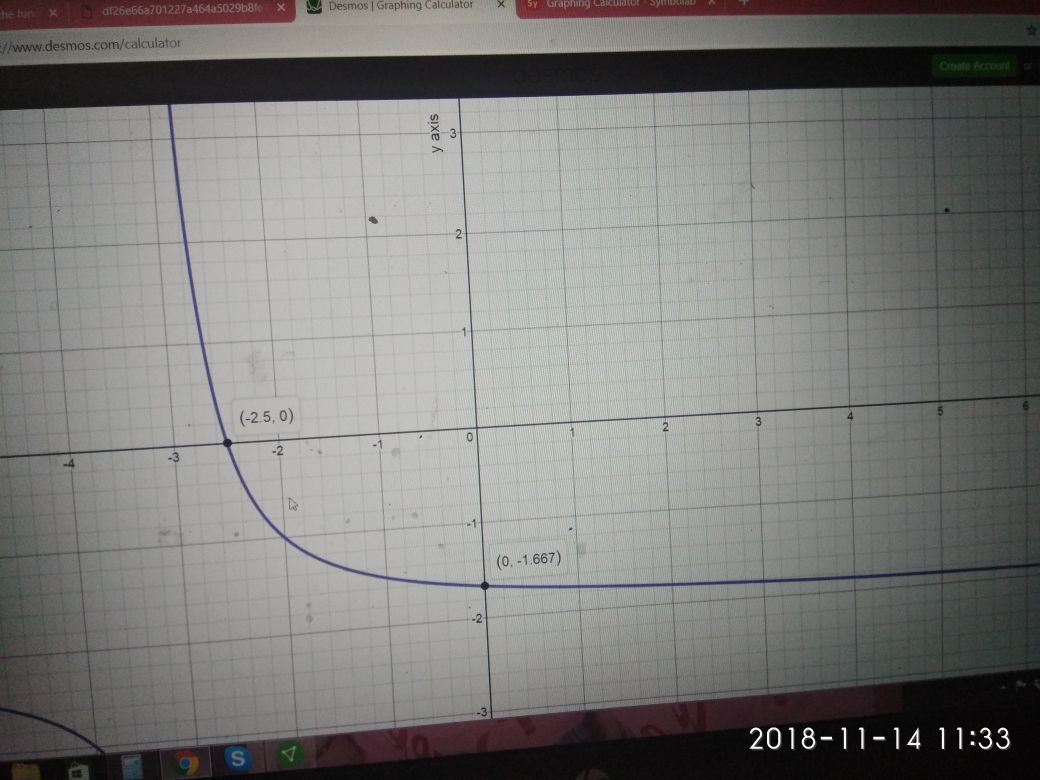
Which graph represents the function f(x) = -|x + 3 ...

30 POINTS) Which graph best represents the function f(x ...

Which graph best represents the function f(x) = (x + 2)(x ...

ラブリーYx2 Graph - 子供向けぬりえ
which graph represents the function f (x)=(3/2)-x ...

View question - Which graph represents the function f(x ...

Which graph represents the function f(x)=2⋅(13)x ...

Image 1: Which graph represents the function f(x)=√x-2−2 ...

0 Comment to "Graphs Of Exponential Functions"
Post a Comment